高等数学
重点难点积分公式
如你所见,这是一个链接:https://zh.wikipedia.org/wiki/积分表
常用积分公式:
等价无穷小
当x → 0,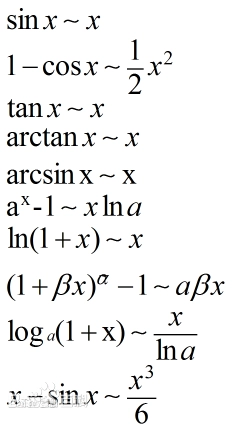
用处:洛必达法则(在极限存在的情况下,分子分母都无穷小或无穷大,则分子分母同时分别求导),
大多可用taylor公式(taylor公式:f(x) = f(0) + f'(0)x + f''(0)/2!x^2 + ... + O(x^n))
空间解析几何
右手坐标系
证明三个向量共面:(a ⨯ b) · c = 0
平面方程表达式:
点法式:A(x-x0) + B(y-y0) + C(z-z0) = 0
一般式:Ax + By + Cz + D = 0
截距式: + + = 1
点面距离公式形式和点线一致
空间曲线切向量:xyz三个方向关于t(或者x)的导数,用于切线方程、切平面方程
空间曲面法向量:xyz三个方向的各自偏导数(梯度),用于切平面方程、法线方程
一般式:Ax + By + Cz + D = 0
截距式: + + = 1
一些基础解题模板,不会不行,不懂就不懂,用就对了😥
求二元函数极值:两个偏函数等于零 求出驻点,分别在每个驻点上 ———— A = fxx(x0,y0),B = fxy(x0,y0),C = fyy(x0,y0),B2-AC < 0,则有极值,其中A>0则为极小值。
链式法则的熟练运用:换元,一些证明题,尤其是那个u = 根号下x^2+y^2 这玩意,它的偏导可以表示成 x/u
级数求和函数:二话不说,先求导或者积分,尤其注意exx = (求和)xn/n!,看到 n! 就要想泰勒公式
证明收敛:拆分成收敛,比较(直接放缩 或者 用比值与0比较)(p级数,1/n是发散),积分(积分有上界),比值(下一项和这一项比值 的极限小于1),根值(比1小发散)
一些个人解题思想,🫥🪽
第一,不要畏难,其实积分的很多题和高中导数的一些题型很相似,只是积分看着很大一坨,实际上先把问题拆分来看,积分只是其中的一环,其他的在高中的时候你就会了。
全增量、全微分
在微积分中,函数f在某一点的全微分(英语:total derivative)是指该函数在该点附近关于其自变量的最佳线性近似。与偏微分不同,全微分反映了函数关于其所有自变量的线性近似,而非单个自变量。
全微分可以看成是把单变量函数的微分推广到多变量函数上:单变量函数的全微分与其微分相同;而多变量函数在某点的全微分为一线性映射,通常可用矩阵或向量表示。
充分条件:
必要条件:对于二元函数,在该点可微,则在该点的全微分为:


链式法则




方向导数和梯度
方向导数:偏导数的推广,表示某一函数沿着某一方向的变化率。
梯度:其方向是在该点的最快增长方向,其量是在这个方向的增长率。
利用方向导数描述梯度:函数f在P点的梯度grad f是一个向量,它的方向是函数f变化最快的方向,它的模就是函数f在P点的方向导数最大值。
全导数,偏导数,方向导数


二重积分和三重积分
直角坐标系和极坐标系,dxdy=r drdθ,dxdydz=r^2 sinφ drdθdφ
第一类曲线积分:ds = 根号下( 两个关于t的函数的导数 的平方和) * dt
平面第二类曲线积分:参数法(转化为t的定积分):Pdx + Qdy = { P(t) * (关于t的x函数的导数) + Q(t) * (关于t的y函数的导数) } * dt
极坐标:ds = 根号下( 关于θ的r函数的平方 和 关于θ的r函数的导数的平方 之和) * dθ
格林公式:(L封闭、分段光滑、有向,P、Q具有一阶连续偏导)Pdx + Qdy = { (Q关于x的偏导) - (P关于y的偏导) } * dxdy
路径无关定理:不就是格林公式延展的特殊情况(不封闭,但是等式右边为0)吗,此时Pdx + Qdy 具有原函数u(x,y)
联系第一类曲线积分:Pdx + Qdy = { Pcosa + Qcosb } * ds 【cosa = (x关于t的函数导数 除以 根号下的各方向的关于t的函数导数的平方和)】
空间第二类曲线积分:参数法(就是变成三个而已),或者斯托克斯公式转化为曲面积分(封闭曲线 or 添加辅助线)
第一类曲面积分:投影法:F(x,y,z)dv = f(x,y,z(x,y)) * (根号下 1 + z关于x的偏导数的平方 + z关于y的偏导数的平方) * dxdydz
第二类曲面积分:投影法:F(x,y,z)dv = ( Pcosa + Qcosb +Rcosc ) dv = Pdydz + Qdxdz + Rdxdy
高斯公式:封闭 分片光滑 外侧 一阶连续偏导数,和格林公式的区别就是全是加法(都是没有的那个微分的偏导)
联系第一类曲面积分:前面有,转换投影(?)
极坐标:ds = 根号下( 关于θ的r函数的平方 和 关于θ的r函数的导数的平方 之和) * dθ
格林公式:(L封闭、分段光滑、有向,P、Q具有一阶连续偏导)Pdx + Qdy = { (Q关于x的偏导) - (P关于y的偏导) } * dxdy
路径无关定理:不就是格林公式延展的特殊情况(不封闭,但是等式右边为0)吗,此时Pdx + Qdy 具有原函数u(x,y)
联系第一类曲线积分:Pdx + Qdy = { Pcosa + Qcosb } * ds 【cosa = (x关于t的函数导数 除以 根号下的各方向的关于t的函数导数的平方和)】
高斯公式:封闭 分片光滑 外侧 一阶连续偏导数,和格林公式的区别就是全是加法(都是没有的那个微分的偏导)
联系第一类曲面积分:前面有,转换投影(?)
散度与旋度(向量分析)
散度与通量,旋度与环量
---------------------------
散度:向量分析中的一个向量算子,将向量空间上的一个向量场(矢量场)对应到一个标量场上。三维空间的散度(且一阶连续偏导):
相关:四元数(散度研究起源),电场力
高斯散度定理(Gauss's Divergence Theorem):空间闭区域Ω是由分片光滑的闭曲面Σ所围起来的三维区域,则有


高斯公式散度表示:


---------------------------
旋度(curl或者记作rot):是一个向量算子,表示在三维欧几里德空间中的向量场的无穷小量旋转。在向量场每个点上,点的旋度表示为一个向量,称为旋度向量。这个向量的特性(长度和方向)刻画了在这个点上的旋转。

相关:四元数,光学场理论
斯托克斯定理:

其旋度表示:











微分方程
几种常见微分方程:
大学物理
第一:积分思想
第二:三维高度
第三:不懂装懂
第四:类比高中
级数
级数(英语:Series)是数学中一个有穷或无穷的序列之和,如果序列是有穷序列,其和称为有穷级数;反之,称为无穷级数(一般也简称为级数)。
柯西审敛准则(在一个完备空间中):对任意的 ,总存在N0>0,使得任意的n>m>N0,
,总存在N0>0,使得任意的n>m>N0,
 ,总存在N0>0,使得任意的n>m>N0,
,总存在N0>0,使得任意的n>m>N0,
调和级数
调和级数(英语:Harmonic series): 
比较审敛法: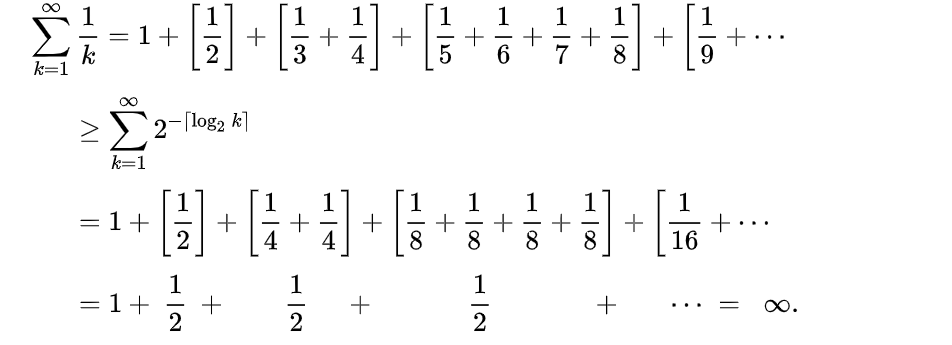
积分判别法(integral test):
反证法: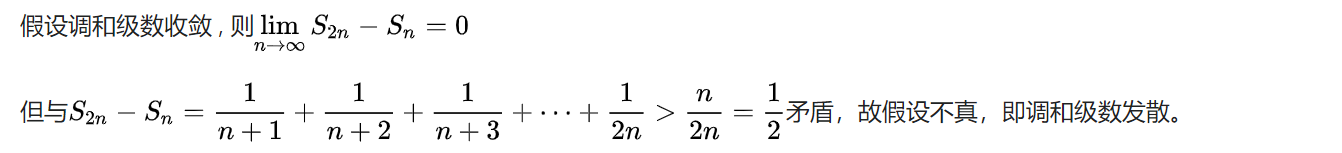
相关级数:
交错调和级数: ;拓展:墨卡托级数(自然对数的泰勒级数形式)、π的莱布尼茨公式。
;拓展:墨卡托级数(自然对数的泰勒级数形式)、π的莱布尼茨公式。
广义调和级数: ,(a!=0,b为实数),由比较审敛法可知广义调和级数全部发散。
,(a!=0,b为实数),由比较审敛法可知广义调和级数全部发散。
p级数: ,p<=1发散,p>1收敛(过饱和调和级数)(其和也就是黎曼ζ函数在p的值)
,p<=1发散,p>1收敛(过饱和调和级数)(其和也就是黎曼ζ函数在p的值)
随机调和级数: ,其中分子是恒等分布的独立随机变量,取值范围为+1和-1,取这两值的概率都是0.5。该级数收敛的概率是1。
,其中分子是恒等分布的独立随机变量,取值范围为+1和-1,取这两值的概率都是0.5。该级数收敛的概率是1。



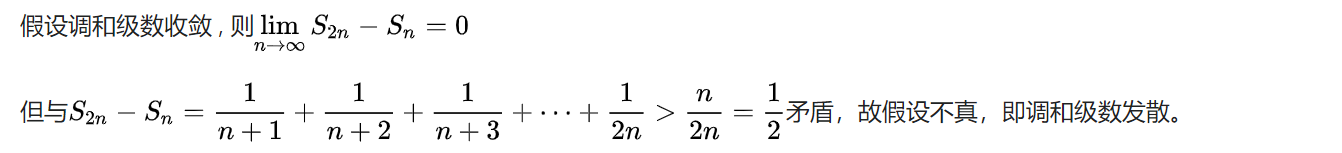
 ;拓展:墨卡托级数(自然对数的泰勒级数形式)、π的莱布尼茨公式。
;拓展:墨卡托级数(自然对数的泰勒级数形式)、π的莱布尼茨公式。 ,(a!=0,b为实数),由比较审敛法可知广义调和级数全部发散。
,(a!=0,b为实数),由比较审敛法可知广义调和级数全部发散。 ,p<=1发散,p>1收敛(过饱和调和级数)(其和也就是黎曼ζ函数在p的值)
,p<=1发散,p>1收敛(过饱和调和级数)(其和也就是黎曼ζ函数在p的值) ,其中分子是恒等分布的独立随机变量,取值范围为+1和-1,取这两值的概率都是0.5。该级数收敛的概率是1。
,其中分子是恒等分布的独立随机变量,取值范围为+1和-1,取这两值的概率都是0.5。该级数收敛的概率是1。
泰勒级数
傅里叶级数






 ;
; ,
, ,
,



 前者为平均数,后者为标准差。
前者为平均数,后者为标准差。 克鲁斯克尔算法(英语:Kruskal's algorithm)
克鲁斯克尔算法(英语:Kruskal's algorithm)